https://www.twahoudini.com/course/rigidbody1
HOUDINI1_ RIGIDBODY
3️⃣ 출동 SIMULATION 기초 이론부터 심화된 내용을 공부합니다. 또한 자동차를 이용한 리깅 시뮬레이션 BASIC을 훈련합니다.
www.twahoudini.com
지난 강의에서는 Constraint의 기본 개념에 대해 공부하였다.
Constraint의 핵심은 물체와 물체 사이의 관계였다. 그 중에서도 강한 복원력을 가지는 관계인 Hard Constraint Relationship을 배웠었다.
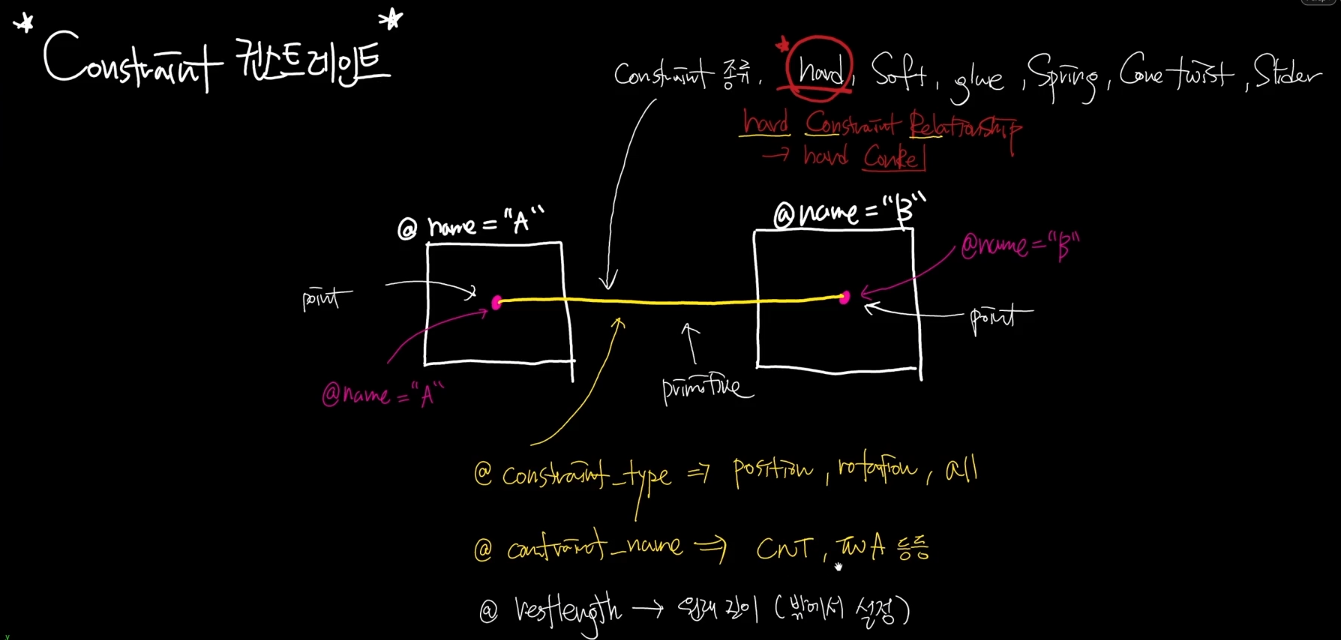
몇 가지 중요한 점을 읊어보고 가겠다.
1. Constraint는 점과 선으로 이루어져 있다. 점에는 어떤 물체를 대변하는지 알려주기 위해서 이름을 가지고 있어야 하고, 이 이름은 해당 Object가 가진 이름과 같아야 한다.
2. 선이 가진 실질적인 관계를 Constraint라 할 수 있다. 그래서 어떤 것을 고정할지 @constraint_type을 정해주어야 했다. 만약 Type이 Position이라면 상대거리를 고정하는 것이고, Type이 Rotation이라면 상대각도를 고정, Type이 All이라면 상대거리와 각도를 모두 고정한다.
3. @constraint_name(관계의 이름)도 직접 정해주어야 했다. 우리는 Connect를 줄여 cnt라고 이름을 사용하였었다.
4. @restlength(Constraint의 원래 길이)가 밖에서 미리 정해진다면, Dop Network 안에서 그 길이를 인지하고, 그 길이에 맞게 복원하려 할 것이다.
만약 @restlength가 미리 정해져있지 않다면, Dop Network는 모든 Constraint가 @restlength =1이라고 판단하여 길이가 늘어나거나 줄어드는 현상을 확인할 수도 있었다.
Rigidbody12에서는 진자 운동에 대해 다루어볼 예정이다. 필요한 개념을 먼저 공부한 뒤 직접 예제를 만들어보도록 하겠다.
목차
1. @active, @animated, @deforming
2. 진자 운동
3. 갯수 늘리기
1. @active, @animated, @deforming

오늘의 목표는 충돌에 의해 좌우 끝에 있는 공들이 움직이는 진자 운동을 구현하는 것이다.
해당 내용을 구현하기 위해서 필요한 내용이다.
추가 어딘가에 매달려있는 것처럼 묘사해주어야 하는데, 이를 밑의 무거운 추와 위의 고정해둔 두 개의 점 그리고 Constraint로서 선을 이용해주려 한다.
이때 Simulation을 실행하면 아래의 추는 중력에 의해서 움직이지만 위의 두 점은 Simulation에서 Object의 역할은 하지만 움직이지 않는다. 이걸 구현하기 위해서 새롭게 @active라는 Attribute를 배울 것이다.
오늘 강의의 시작은 RigidBody Simulation에서 이용되는 Attributes를 좀 더 다양하게 이해하는 것부터이다.

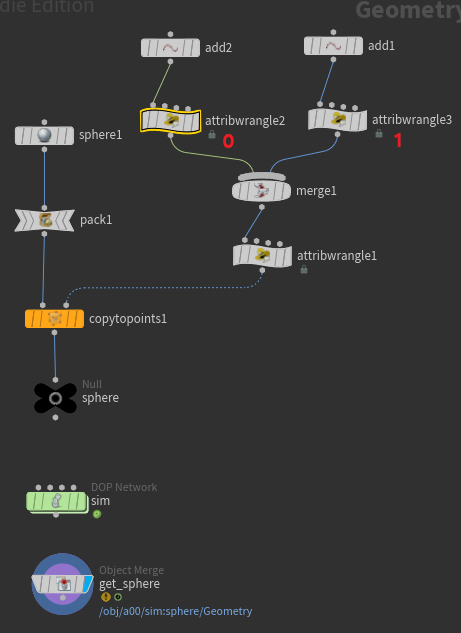
먼저 쉬운 RigidBody Simulation 세팅에서 새롭게 배울 Attributes을 보겠다.
오늘 배울 Attributes는 @active, @animated, @deforming이다.
@active는 RBD Packed Object에 올려둔 물체가 Simulation의 영향을 받느냐의 여부를 정하는 Attributes이다. 만약 Simulation의 영향을 받는다면 우리가 세팅해둔대로 중력에 의해 떨어져 지면과 충돌하게 될 것이다. 그런데 만약 Simulation의 영향을 받지 않는다면 움직이지 않을 것이다.
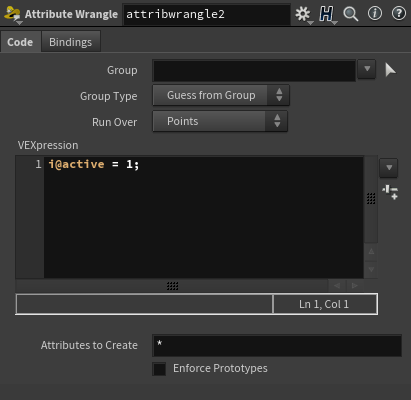
방금 말한 Simulation의 영향을 받는다는 상황이 바로, "i@active = 1"일 때의 상황이다.
지금 아무런 active에 대한 세팅도 없는 상황에서 Simulation을 작동시켰을 때 Sphere가 Simulation의 영향을 받는 것을 보면, 기본적으로 Sphere의 active는 1로 세팅되어 있는 것을 알 수 있다.
Attribute Wrangle을 각각의 points 아래에 달아 한쪽 active 값은 1로, 다른 한쪽은 0으로 정의하겠다.
Simulation을 실행시키면 active를 1로 지정해둔 쪽의 공만 중력의 영향을 받는 것을 볼 수 있다.

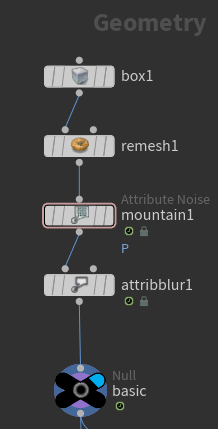
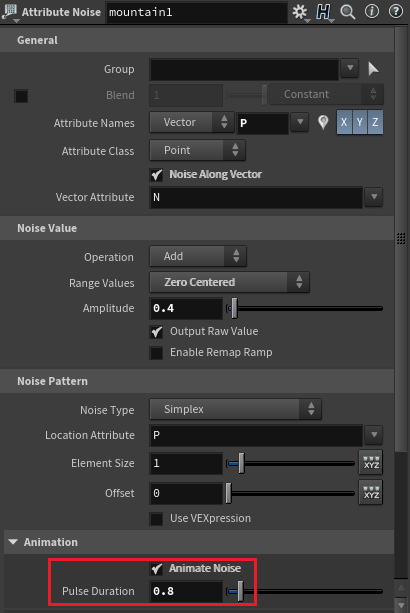
이제 @animated와 @deforming을 알아보기 위해서 새롭게 세팅을 잡아주겠다.
시시각각 모양이 변하는 Box가 날아가 벽에 부딪히는 Simulation을 만들어보겠다.
Box를 생성해 Remesh, Mountain, Attribute Blur로 Noise Animation이 들어간 Object를 만들어준다.
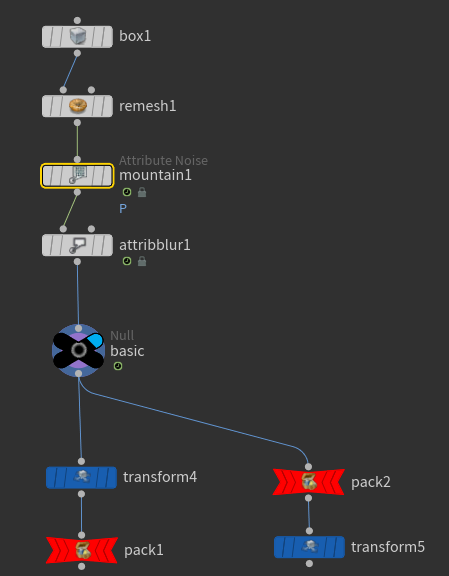
그 다음 Pack과 Transform을 꺼내준다.
우리는 Box가 벽쪽으로 움직이게 하기 위해서 Transform을 쓰려 한다. 그리고 Simulation을 위해서 Dop Network의 RBD Packed Object로 물체를 활용할 것을 생각한다면, 어찌되었던 Packing을 하는 과정이 필요하다.
이때 이동에 대한 Tranform을 먼저하고 Pack을 하는가, Pack된 물체를 Transform으로 옮기는가에는 차이가 있다. 두 node가 놓이는 순서에 따라 결과도 달라진다.
그리고 우리가 앞으로 배우게 될 @active, @animated, @deforming을 다룸에 있어서도 두 순서에서의 결과엔 차이가 있다.

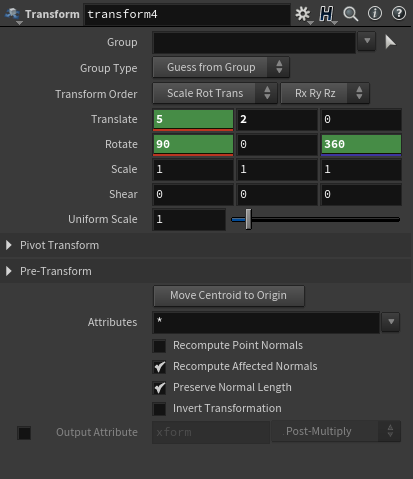
각각의 Transform에 Animation을 잡아준다.
각각의 결과의 차이를 보기 위해서 Simulation을 실행시켜 비교해보겠다.
겉으로 보이는 결과에는 둘은 같아보인다. 그러나 둘은 완전히 다른 내용을 가지고 있다.
자세한 설명은 이후에 하고 먼저 필요한 세팅들부터 만들어보겠다.
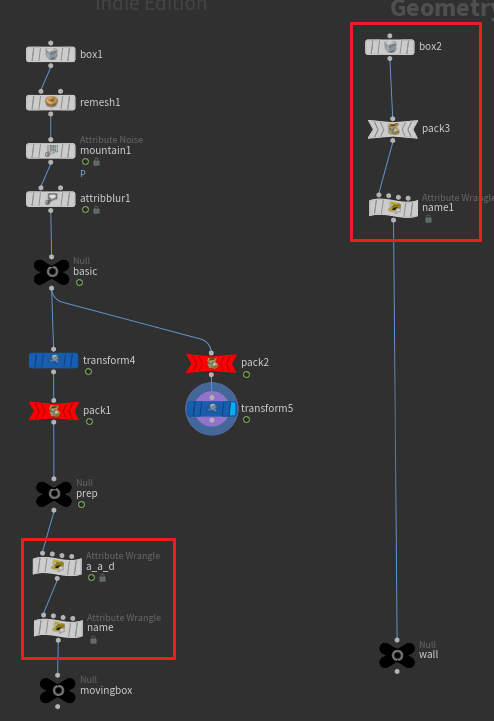
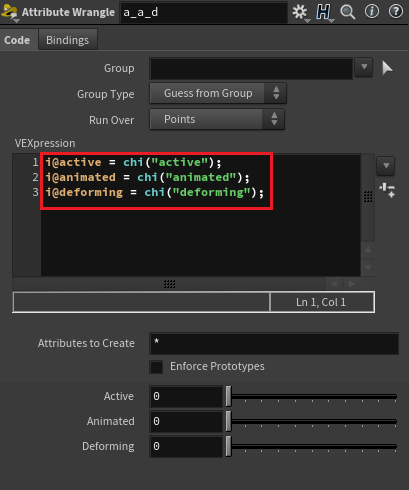
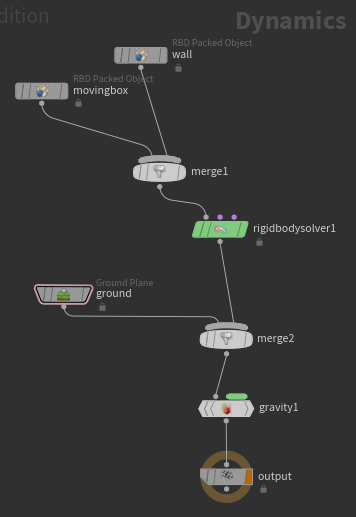
@active, @animated, @deforming를 설정해줄 Attribute Wrangle과 @name을 지정해줄 Attribute Wrangle을 생성한다.
그리고 충돌 물체로 이용될 벽도 만들어준다. Box를 Pack한 뒤 @name을 정해준다.
그리고 Dop Network 안에서 RigidBody Simulation을 세팅해준다.
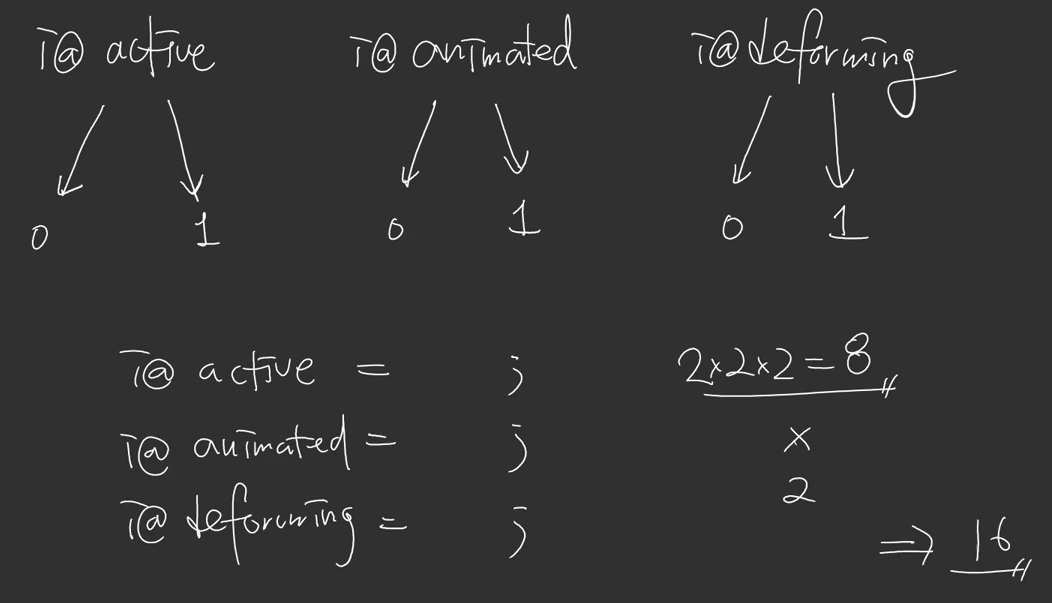
이론 설명이다.
앞서 설명한 @active와 마찬가지로 @animated와 @deforming도 0과 1로 작동을 조절할 수 있다.
이때 우리는 이 세가지 Attributes들을 이용해 2*2*2=8 가지의 경우의 수를 만들어낼 수 있다. 거기에 앞서 세팅해둔 Pack과 Transform의 두 가지 순서의 경우까지 생각해준다면 총 16가지의 경우의 수가 만들어진다.
너무 많다고 생각할 수 있지만, 이 16가지의 경우의 수에서 일반적으로 쓰이는 조합은 몇 가지 없다.
이때 @animated와 @deforming이 무엇인지 알기 위해서는 Pack과 Transform의 두 가지 순서에 대한 결과를 이해해야 한다.

새로운 Geometry에서 Box가 이동하는 간단한 세팅을 만들어준다.
이때의 Pack되지 않은 Box는 Animated되기 보다는 Deforming되었다고 보는게 맞다. 물체의 모양이 시시각각 바뀌고 있다고 보는 것이 맞다.
우리가 Transform에서 시간에 따라 값이 바뀌게끔 KeyFrame을 준 행위는 Animation을 준 것이 맞다. 그러나 결과 자체로 생각하자면 물체가 Deforming, 아예 변형이 되고있다고 할 수 있다. 왜냐하면 시간에 따라 위치 정보가 바뀌고 있기 때문이다.
하지만 움직이는 물체는 전부 Deform이 되고 있는 것이라고는 볼 수 없다. Object를 RBD Packed Object에서 쓰기 좋게 Pack한 상태에서 Deforming이 되는 것인지, 아니면 Animated된 것인지 분류해야 한다.
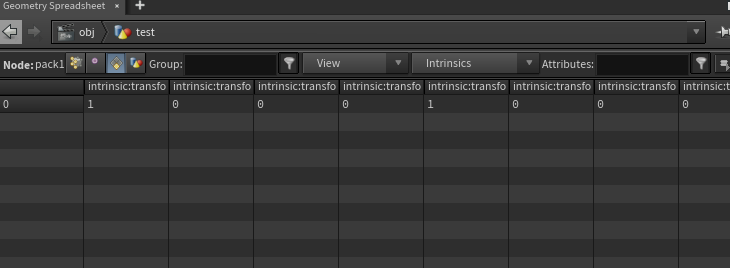
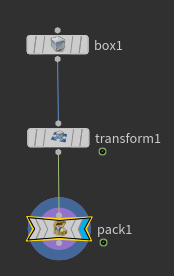
Box 아래에 Pack을 달아주겠다.
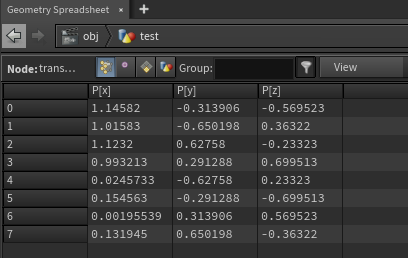
이때 결과가 Animated된 결과인지 Deforming된 것인지를 알고 싶다면, Primitive의 Intrinsics:transform을 보면 된다.
만약 Intrinsics:transform 정보가 Box가 움직이는 동안 조금이라도 바뀐다면, Animated된 상태라고 볼 수 있다.
만약 Intrinsics:transform 정보가 하나도 바뀌지 않는다면, 이건 Deforming되고 있는 것이라고 볼 수 있다.
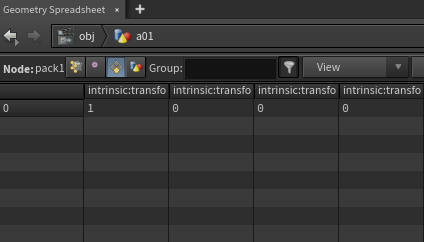
Transform 다음 Pack이 된 결과를 보면, Intrinsics:transform의 정보가 바뀌지 않은 것을 보아 Deforming 되었다고 볼 수 있다.
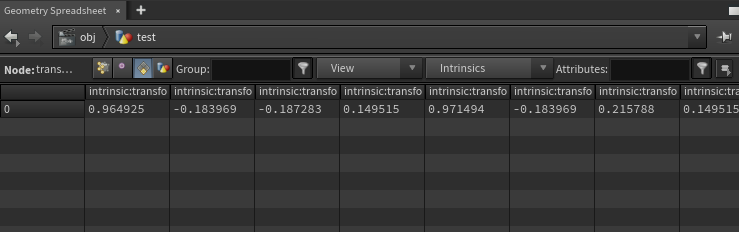
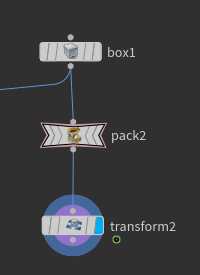
이번에는 먼저 Pack을 해준 뒤 Transform으로 Animation을 주겠다.
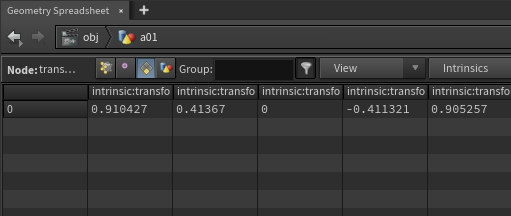
결과를 보면, Intrinsics:transform의 정보가 시시각각 바뀌고 있는 것을 보아 Animated 되었다고 볼 수 있다.
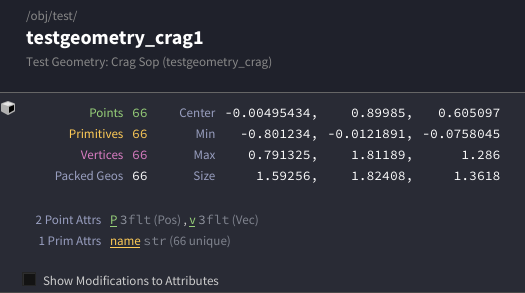
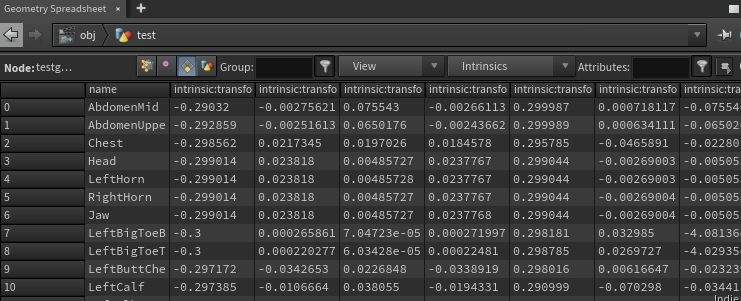
이번에는 Crag를 꺼내어 Animated된 결과인지, Deforming된 결과인지를 확인해보겠다.
Node Info를 보면 66개의 Packed Geo가 있는 것을 볼 수 있다. 또한 이미 Animation이 적용된 것을 볼 수 있다.
결과를 보면, Intrinsics:transform의 정보가 시시각각 변하고 있기 때문에 Animated 되었다고 이해할 수 있다.
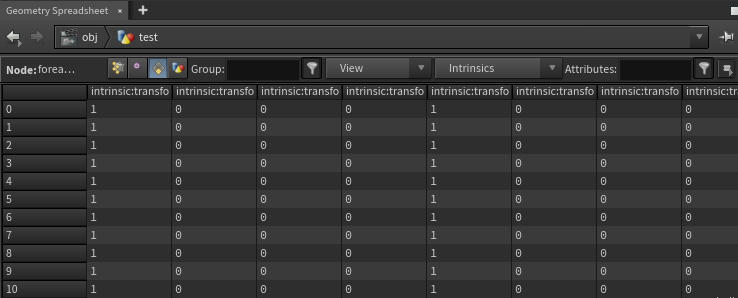
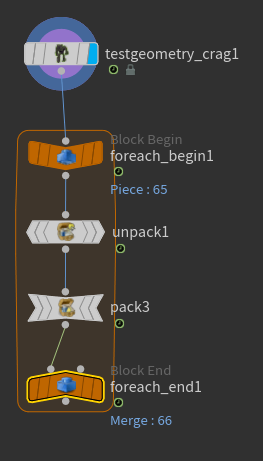
For-each Primitive로 Crag에서 각각의 조각들을 Unpack해준 뒤 다시 Pack 해주는 과정을 거쳐준다면 결과가 어떻게 바뀔지 보겠다.
결과를 보면, Intrinsics:transform의 정보가 바뀌지 않은 것을 보아 Deforming 되었다고 볼 수 있다.
다시 a01에서 작업하도록 하겠다.
Intrinsics:transform을 보면 Transform - Pack은 Animated된 것이 아니라 Deforming된 상태라 할 수 있다.
Intrinsics:transform을 보면 Pack - Transform은 Deforming된 것이 아니라 Animated된 상태라 할 수 있다.
이때 Pack - Transform의 결과는 원본의 모양도 계속 바뀌고 있기 때문에 해당 결과는 Animated 되었으면서, Deforming도 발생하고 있다고 할 수 있다.
하지만 Transform - Pack의 결과는 Animated 없이 오로지 Deforming만 발생하고 있다고 볼 수 있다.


이제 @active, @animated, @deforming을 미리 만들어서 물체를 Dop Network에 넣는 이유에 대해 설명해보겠다.
중력이 작용하고 있는 Simulation에서 각각의 Attributes의 조건이 변할 때 어떻게 Simulation이 작동될지를 보겠다.
먼저 @active가 0일때, Transfom - Pack의 결과부터 보겠다.
0,0,1의 결과에서는 중력의 영향을 받지 않고 Dop Network 밖에서 준비한 움직임을 따라가면서 벽과 충돌하는 것을 볼 수 있다.
0,1,0에서는 애초에 Animated가 되지 않았던 물체이기에 움직이지 않는 것을 볼 수 있다.
0,1,1의 결과에서도 움직이지 않는 것을 볼 수 있는데, 이는 @animated와 @deforming 모두 1인 것은 올바른 설정이 아니기 때문이다. 둘 중 하나만 1이어야 작동을 한다고 볼 수 있다.



이번에는 Pack - Transform의 결과를 보겠다.
0,1,0의 결과에선 우리가 원했던대로 Box가 날아가 벽에 충돌하는 상황이 묘사되고 있다. 하지만 Box의 면이 Noise에 의해 움직이지는 않는 것을 볼 수 있다.
0,0,1의 결과에서는 기대했던대로 Box가 날아가 벽에 충돌하는 상황이 묘사되고 있다. 또한 Box의 면이 Noise에 의해 Deforming 되는 것 또한 볼 수 있다.
0,1,1에서는 역시 움직이지 않는 것을 볼 수 있다.


다음은 @active가 1일때, Transform - Pack의 결과를 보겠다.
1,1,0에서는 Box가 중력에 의해 바닥에 떨어지기만 하는 것을 볼 수 있다. Animated에 대한 정보가 없기 때문이다.
1,0,1에서는 Box가 중력에 의해 떨어지면서 Deforming의 영향을 받아 이동하고 있는 것을 볼 수 있다.


Pack - Transform에서의 결과를 보겠다.
1,1,0에서는 Animated가 주어지지 않을 때와 똑같이 바닥에 떨어지기만 하는 것을 볼 수 있다.
1,1,1의 결과에서도 @animated, @deforming이 작동하지 않아 바닥에 떨어지기는 Box를 볼 수 있다.
1,0,1에서는 Box가 Deforming에 의해 꿀렁거리면서 Animation의 정보 또한 잘 적용된 것을 볼 수 있다.
이렇게 가능한 모든 경우의 수를 다 보았다. 이제 신경써야할 건 우리가 준비한 물체를 의도에 맞게 Dop Network에 로드할 수 있느냐이다.

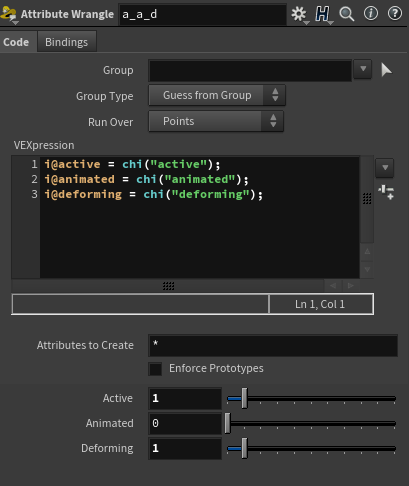
Crag를 @active, @animated, @deforming을 활용해 만든 상황이다.
2. 진자 운동
이제 진자 운동 예제를 배워보겠다.
지금부터 다시 수업의 핵심이 Constraint로 돌아온다. 앞에서 배운 내용은 기본 지식으로 취급하도록 하겠다.
먼저 하나의 진자만 만들어보겠다.
일단은 핵심이 되는 추와 고정을 위한 Sphere를 만들어 줄 것이다. 추와 Pivot의 이름을 전부 다르게 지어주겠다.
이때 Pivot과 추를 연결해주는 Constraint의 type을 Position으로 두겠다.

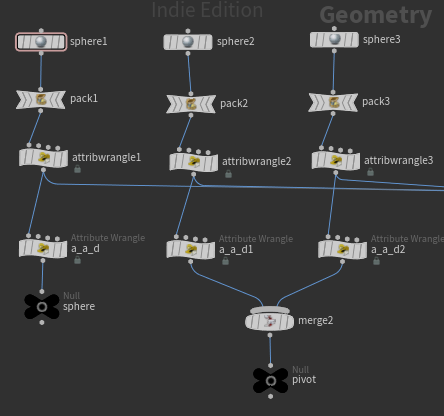
추와 Pivot이 될 Sphere(Primitive)를 세 개 만들어준다.
RBD Packed Object로 불러들이기 위해서, Pack해준 뒤 이름을 지정해준다.
그 다음 Attribute Wrangle을 달아 @active, @animated, @deforming에 대한 정보를 정의해준다.
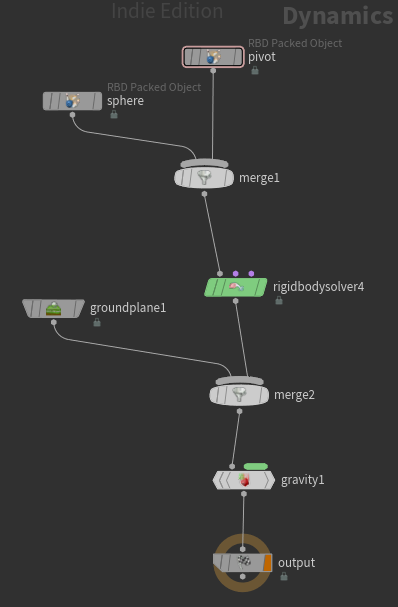
Dop Network를 생성해 그 안에서 RigidBody Simulation 세팅을 해준다.
Simulation이 잘 작동하는지 확인하였다면, 이제 Geometry 단계에서 Constraint에 대한 정보를 생성해주겠다.
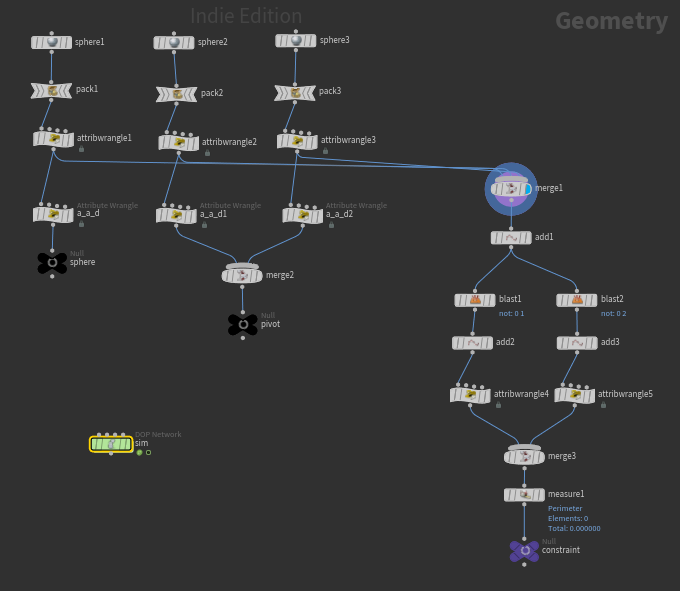
Constraint를 만들기 위해서 점의 정보만이 필요하기 때문에 Add로 Sphere에서 면을 제거해 점만을 남겨주겠다.
그 다음 Blast로 Pivot과 추를 떼어내어 준다. 떼어낸 점들을 각각 Add로 선으로 만들어준다.
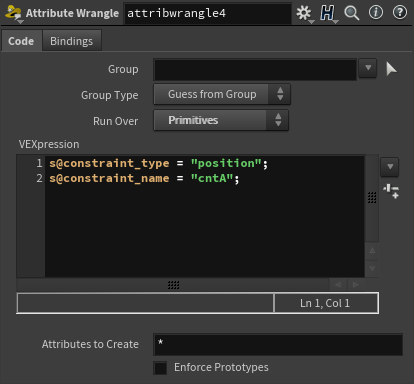
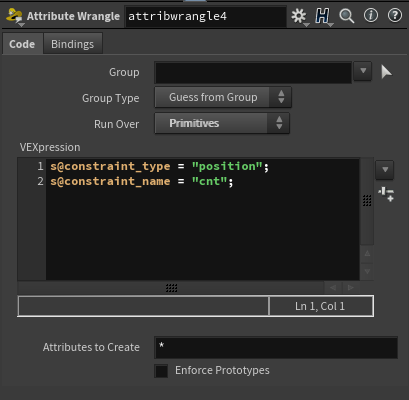
Attribute Wrangle로 @constraint_type과 @constraint_name을 지정해준다. 둘의 이름만 다르게 지정해주고 type은 같게 해준다.
Measure node를 달아 @restlength를 정의내려준다.

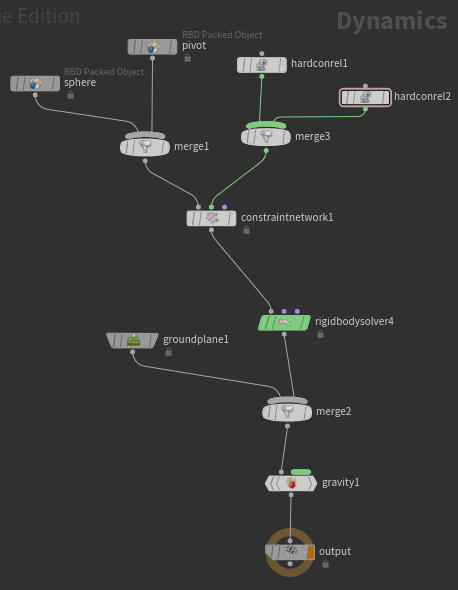
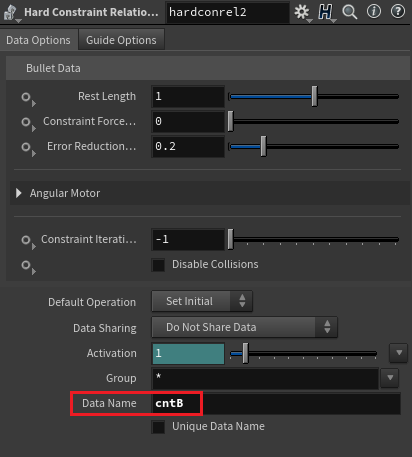
Dop Network 안에서 Hard Constraint Relationship node를 두 개 생성해 Constraint 세팅을 잡아준다.
Simulation을 실행시키면 Pivot에 매달려 가만히 있는 추를 볼 수 있다.

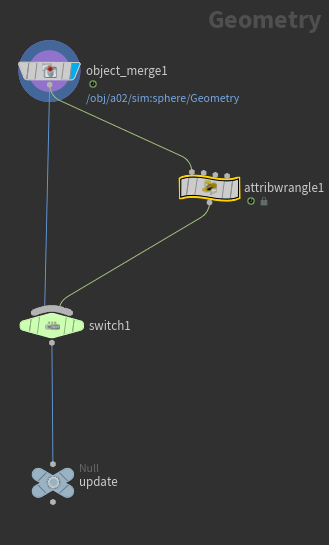
이제 Sphere가 스스로 24 Frame에 어떠한 힘을 받아서 움직일 수 있도록 만들어주겠다.
Sourcing에서 추의 정보가 들어있는 Sphere 그릇에 어떠한 움직임을 추가해주도록 하겠다.
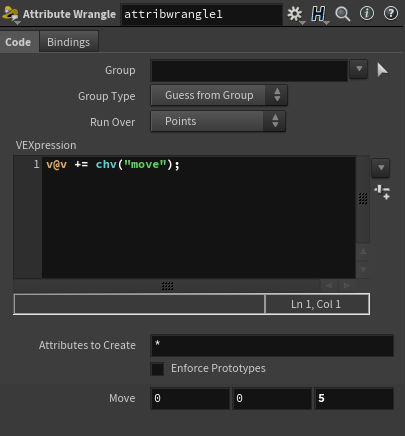
SOP Network에서 Sphere 그릇의 정보를 불러와, Switch를 이용해 24 Frame에 "v@v = {0,0,3}" 값이 들어가도록 해주겠다.
결과를 보면 원했던 대로 Pivot에 고정된 채 좌우로 움직이는 추를 볼 수 있다.
이때 @v의 값을 높여줌으로써 추가 움직이는 속도를 높여줄 수 있다.

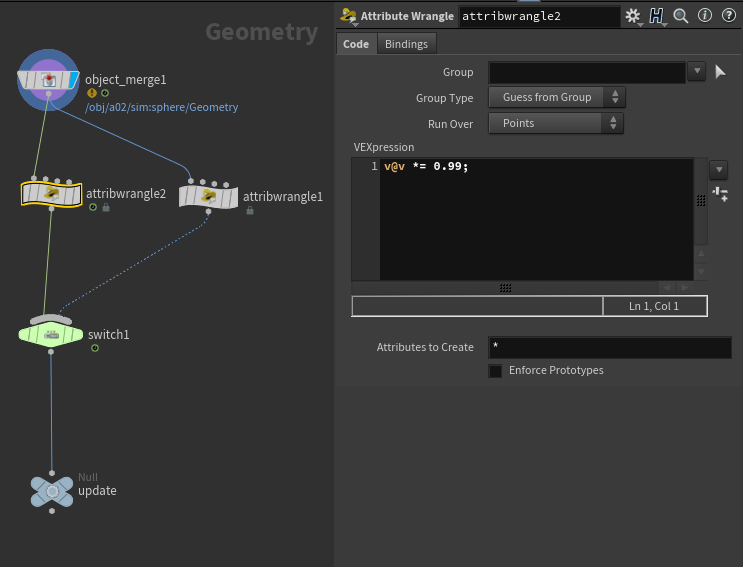
만약 점점 속도가 줄어들기를 원한다면, @v 값에 소숫값을 곱해주어 매 Frame마다 속도가 줄어들도록 해줄 수 있다.
3. 갯수 늘리기
이제 추와 Pivot을 여러개 생성해 진자운동을 하도록 만들어보겠다.
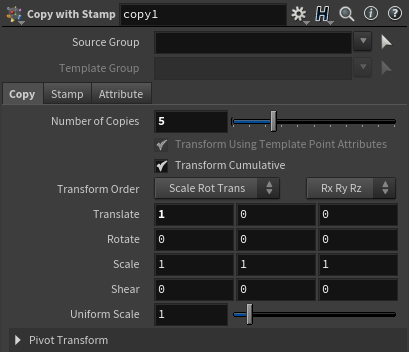

한 점을 생성해준 다음 Copy with Stamp로 그 갯수를 늘려주겠다.
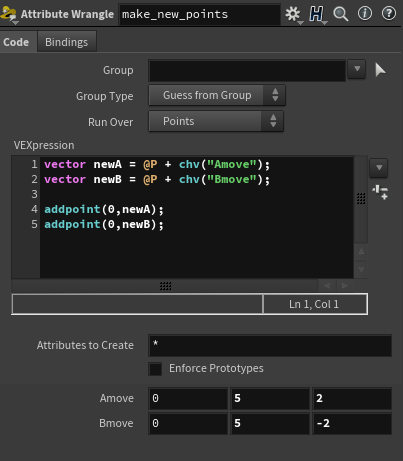
그 다음 For-each point에서 각각의 점의 정보를 이용해 Pivot에 이용될 점을 두 개씩 생성해주겠다.
이제 각각의 point들이 다른 이름을 가지는 것이 중요할 것이고, 추후에 만들 Constraint를 고민해보아야 한다.
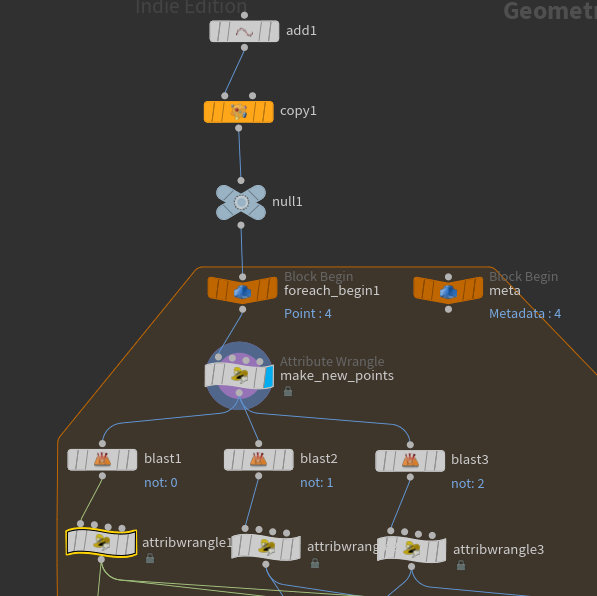
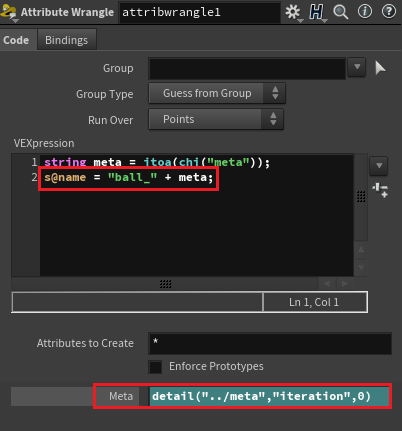
블럭의 반복 Iteration 값을 이용해 이름을 만들고자 한다.
먼저 추와 두 개의 Pivot 각각 따로 이름 작업을 해주도록 하기 위해서 Blast로 떼어내어 준다.
Attribute Wrangle에서 detail function을 이용해 meta에서의 @Iteration 값을 불러와준다. 이때 불러온 @Iteration 값을 itoa를 이용해 String 정보로서 저장해주겠다.
이제 s@name에 앞서 불러온 @Iteration 값을 더해주어 Pass마다 다른 이름이 붙도록 해주겠다.
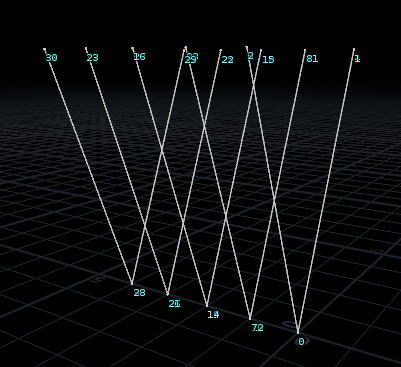
Blast로 떼어낸 다른 point들에도 해당 @name 정보를 붙여준다. base가 될 이름은 전부 다르게 설정해주도록 한다.

그 다음은 각각 추와 Pivot 하나씩 Merge하여 선으로 만들어준다.
이 선들은 Constraint를 만들 때 쓰일 것이다.
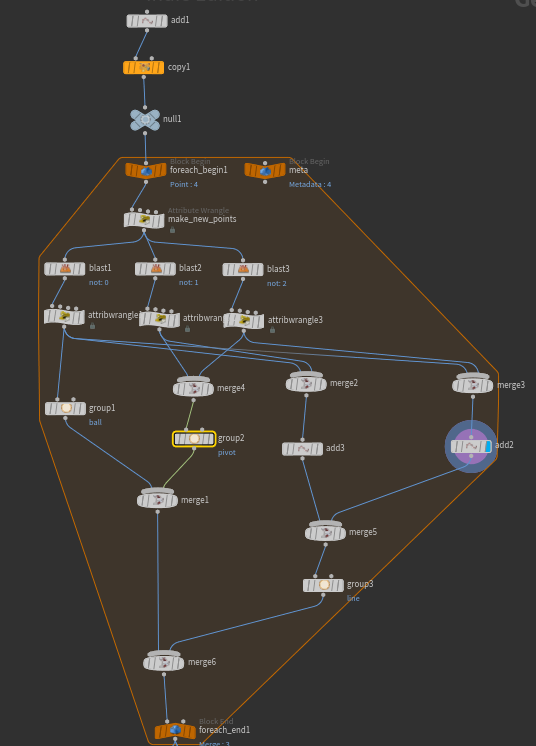
Constraint 정보를 만들기 전 Group으로 정보들을 정리해주고 가겠다.
추에 대한 점을 ball Group으로 만들어준다.
Pivot에 대한 점들을 pivot Group으로 만들어준다.
Constraint가 될 선에 대한 정보는 line Group으로 해주겠다.
Merge로 정보들을 모두 묶어서 Block End에 연결해준다.
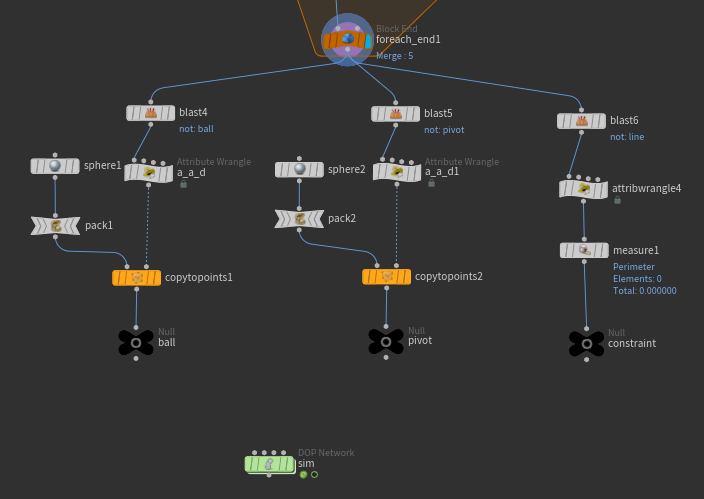
이제 Blast로 Group별로 떼어낸 다음 Copy to Points해주겠다.
그 다음 추와 Pivot에 @active 세팅을 해준다. @active 값을 추는 1, Pivot은 0을 주겠다.
line의 경우는 Attribute Wrangle로 Constraint에 대한 세팅을 해준다. Measure를 달아 @restlength를 정해준다.

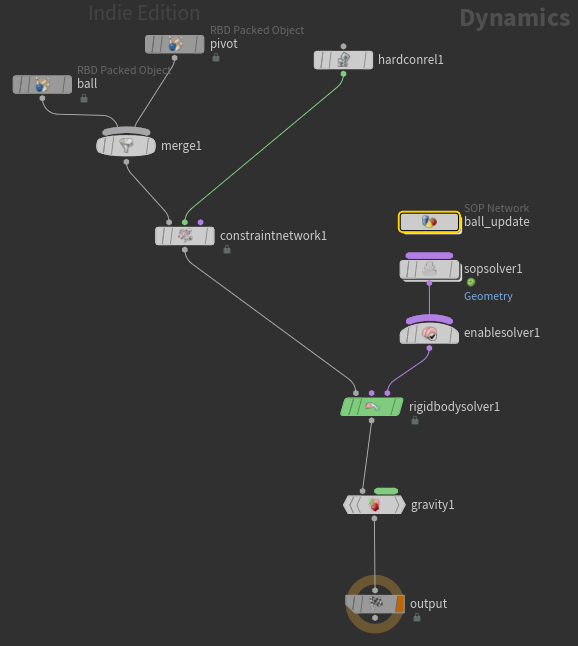
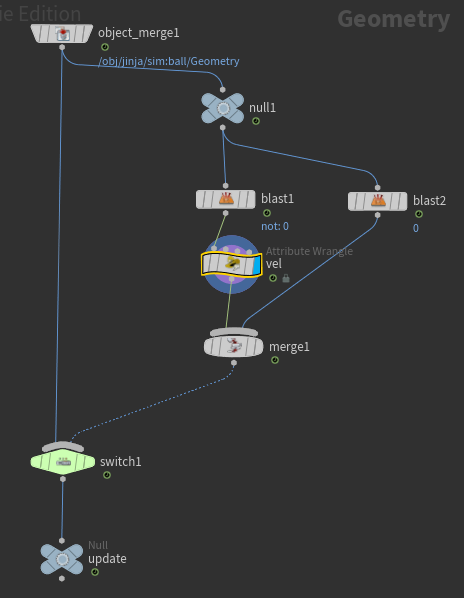
Dop Network 안에서 RigidBody Simulation 세팅을 해주겠다.
Sourcing을 해주어 추가 24 Frame에 움직이도록 해준다. 이때 Blast로 한 점만 떼어내어 v@v 값을 주도록 한다.
결과를 보면 원하는대로 움직이는 것은 성공했지만 추들이 충돌했을 때 아쉬움이 있다.

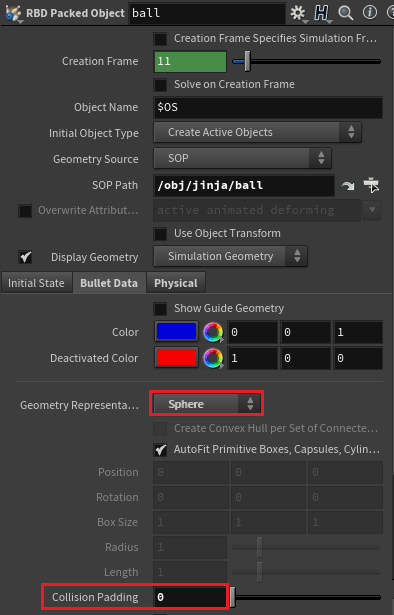
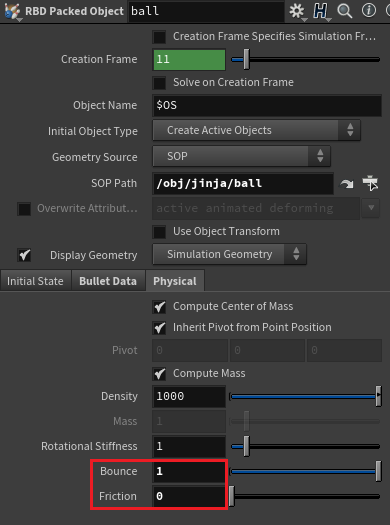
Ball 그릇의 Physical에서의 Bounce와 Physical 값을 각각 1과 0으로 바꿔준다.
그 다음 Bullet Data에서 Convex Hull을 Sphere로 바꿔주고, Collision Padding 값을 0으로 해주겠다.
결과를 보면, 우리가 기대했던 대로 진자 운동을 하는 것을 볼 수 있다.
'TWA Houdini1 > Rigidbody' 카테고리의 다른 글
| TWA 후디니 1 RIGIDBODY_14_01 : 의자 다시 만들기 (0) | 2023.04.07 |
|---|---|
| TWA 후디니 1 RIGIDBODY_13 : Glue, Hard, Soft Constraint 기본기 (0) | 2023.04.07 |
| TWA 후디니 1 RIGIDBODY_11 : Constraint 기본 개념 (0) | 2023.04.06 |
| TWA 후디니 1 RIGIDBODY_09 : 총알+레고+플랭크 소싱으로서 시뮬레이션하기 (0) | 2023.03.31 |
| TWA 후디니 1 RIGIDBODY_08 : Procedural lego modeling (0) | 2023.03.31 |